在计算物体旋转时,如相机标定中的旋转矩阵R,通常都是以三维矩阵表示,三个自由度分别是绕三个坐标轴的旋转角度,但在Unity中,或者像colmap中,都是以四元数(Quaternion)来表示三维旋转的。实际上是复平面向量与实数域矩阵的一个转换关系,这里推导一下。
二维情况
一维数轴上的复数对应于一个二维实数空间,比如一个二维空间坐标为 $(x,y)$ 的复数表示为 $x + yi$ 。
给定两个复数 $z1 = a + bi$, $z2 = c +di$, 其乘积可以表示为:
$$ z1z2 = (a+bi)(c+di) = (ac-bd)+(ad+bc)i $$
对于向量$z2$,与$z1$的乘积可以表示为矩阵形式,即:
$$
\begin{bmatrix}
a & -b \\
b & a \\
\end{bmatrix}
\cdot z2
$$
如果将$z2$也看做一个变换表示成矩阵形式,则
$$
z1z2 =
\begin{bmatrix}
a & -b \\
b & a \\
\end{bmatrix}
\cdot
\begin{bmatrix}
c & -d \\
d & a \\
\end{bmatrix}
$$
此时满足交换律。
二维旋转
设向量模长为1,即$\sqrt[2]{a^2 + b ^2} =1$,则$a = cos\theta, b=sin\theta$, 则对一个向量$\vec{v}=x+yi$,其乘积为$\vec{v} \dot z = (xcos\theta -ysin\theta) +(xsin\theta +ycos\theta)i$,
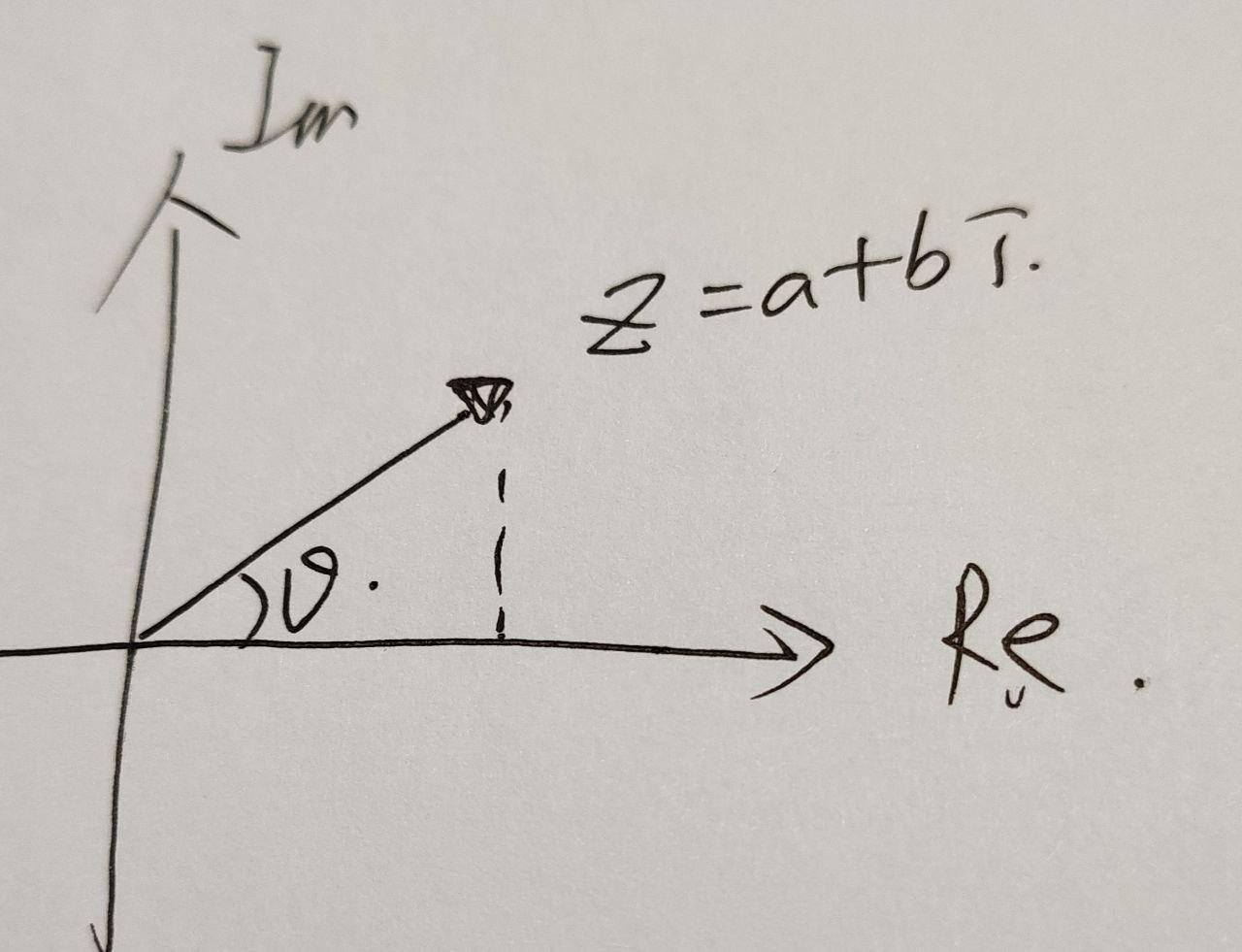
设向量$\vec{v}$的模为r,则$\vec{v}\cdot \vec{z} = r(cos\theta_1cos\theta_2 -sin\theta_1sin\theta_2)+r(cos\theta_1sin\theta_1 + sin\theta_1cos\theta_2)i = rcos(\theta_1 +\theta_2) +rsin(\theta_1 + \theta_2) i $
可以看出,一个单位的二维向量,或一维复数,可以表示成一个旋转变换,即逆时针旋转$\theta$角。
所以二维的旋转矩阵可以很直观的求得:
$$
\begin{bmatrix}
cos\theta & -sin\theta \\
sin\theta & cos\theta \\
\end{bmatrix}
$$
极坐标形式
其实将复数表示成极坐标形式,欧拉公式将三角函数和复平面关联起来,于是可以很直接的将$ e^{i\theta} = cos\theta + isin\theta$带入,角度旋转即$$ e^{i\theta_1} * e^{i\theta_2} = e^{i(\theta_1 + \theta_2)}$$
三维情况
先看向量的旋转: 将向量$\vec{v}$绕旋转轴$\vec{u}$旋转$\theta$角。
将$\vec{v}$分解成两个正交向量的和,分别是平行于$\vec{u}$和垂直于$\vec{u}$的向量,记为$\vec{v_{||}}$和$\vec{v_\bot}$,平行的向量旋转不变,因此只需要考虑垂直向量即可。
对于$\vec{v_{||}}$,其实就是在$\vec{u}$上的正交投影,因此有$\vec{v_{||}} = \frac{\vec{u}\cdot \vec{v}}{||\vec{u}||^2} \vec{u}$,设$\vec{u}$为单位向量,则可以表示为$\vec{v_{||}} = (\vec{u}\cdot \vec{v})\vec{u}$ 。
所以,$$\vec{v_\bot} = \vec{v} - \vec{v_{||}} = \vec{v} - (\vec{u}\cdot \vec{v})\vec{u}$$
因为$\vec{v_\bot}$和$\vec{u}$垂直,所以旋转可以转化成二维平面的旋转,构造一个向量$\vec{w} = \vec{u} \times \vec{v}$,如图所示,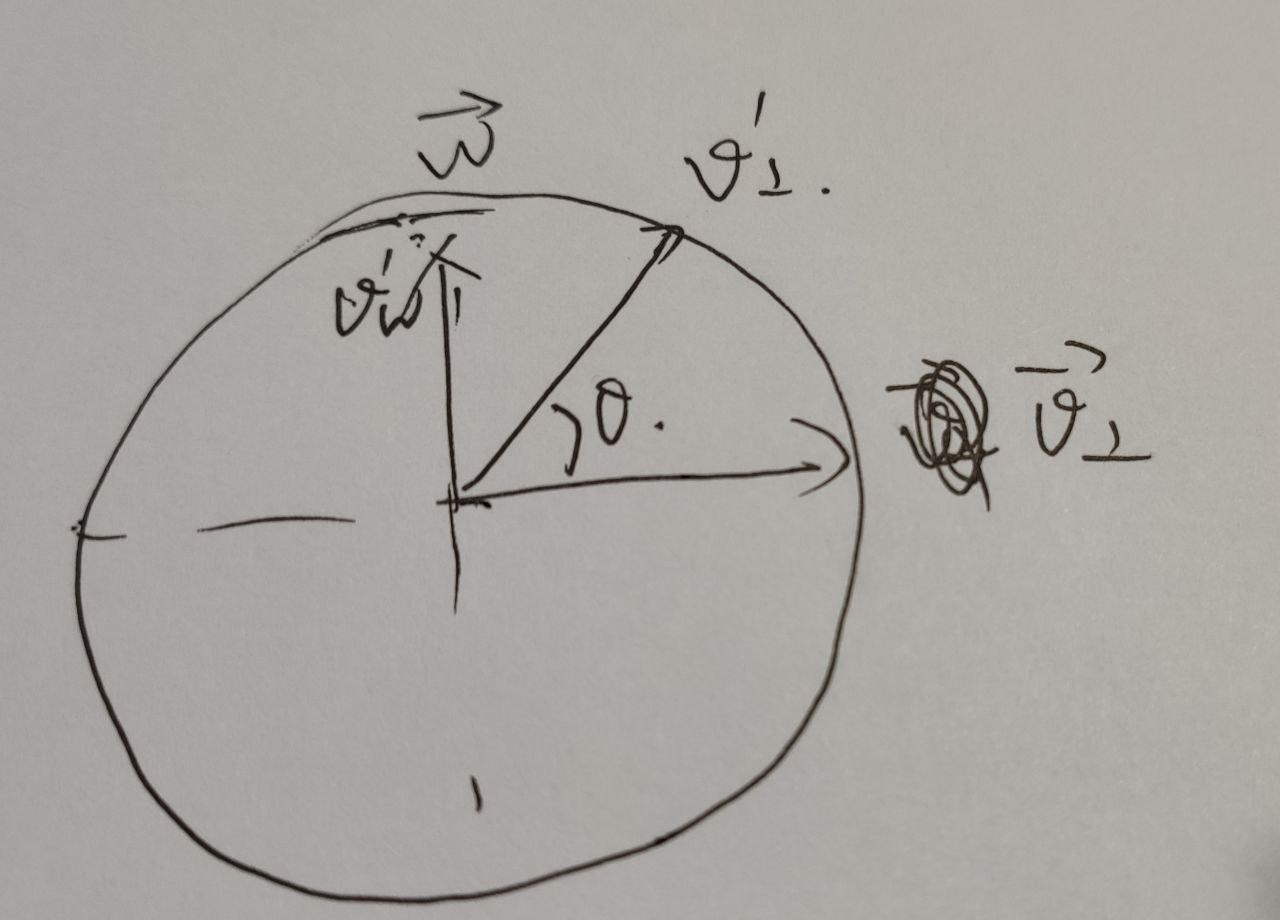
所以旋转后的向量为$$\begin{aligned} \vec{v_\bot}^\prime & = \vec{v_\bot}cos\theta + \vec{w}sin\theta \\ & = \vec{v_\bot}cos\theta + \vec{u} \times \vec{v_\bot} sin\theta \end{aligned}$$
最后旋转后的向量为 $$ \begin{aligned} \vec{v}^\prime & = \vec{v_{||}} + \vec{v_\bot}^\prime \\ & = \vec{v_{||}} + \vec{v_\bot}cos\theta + \vec{u} \times \vec{v_\bot} sin\theta \\ & = (\vec{u}\cdot \vec{v})\vec{u} + \vec{v_\bot}cos\theta + \vec{u} \times \vec{v_\bot} sin\theta \\ & = (\vec{u}\cdot \vec{v})\vec{u} + (\vec{v} - (\vec{u}\cdot \vec{v})\vec{u} )cos\theta + \vec{u} \times (\vec{v} - (\vec{u}\cdot \vec{v})\vec{u}) sin\theta \\ & = \vec{v}cos\theta +(1-cos\theta)(\vec{u}\cdot \vec{v})\vec{u} +(\vec{u}\times \vec{v}))sin\theta \end{aligned}$$
四元数
四元数可以看做一个四元向量,或是有三个虚部的复数,如$q = a + bi+cj+dk$,也可以写成矩阵形式,
$$\vec{q} =
\begin{bmatrix}
a \\
b \\
c \\
d \\
\end{bmatrix}
$$
如三维坐标轴的顺序,复数相乘有,
$$ij =k \\
jk =i \\
ki =j$$
令$q1 = a + bi+cj+dk$, $q2 = e + fi+gj+hk$
则左乘$q1$可以为
$$
\begin{aligned}
q1q2 & = ae + a f i + agj + ahk + \\
& bei − b f + bgk − bhj + \\
& cej − c f k − cg + chi + \\
& dek + d f j − dgi − dh \\
& = ( ae − b f − cg − dh )+ \\
& ( be + a f − dg + ch ) i \\
& ( ce + d f + ag − bh ) j \\
& ( de − c f + bg + ah ) k
\end{aligned}
$$
矩阵形式可以写成,
$$q1q2 =
\begin{bmatrix}
a & -b & -c & -d \\
b & a & -d & c \\
c & d & a & -b \\
d & -c & b & a
\end{bmatrix}
\begin{bmatrix}
e \\
f \\
g \\
h \\
\end{bmatrix}
$$
四元数向量不满足交换律,右乘会有一些区别。
Graßmann积
将四元数的虚部表示成一个向量,即$ q1 = [a,\vec{v}]$,$q2 = [e, \vec{u}]$,其中,$\vec{v} = bi+cj+dk$,$\vec{u} = fi+gj+hk$。
则左乘$q1$可以化简成
$$q1q2 = [ ae − \vec{v} \cdot \vec{u} , a\vec{u} + e\vec{v} + \vec{v} \times \vec{u} ]$$
这个结果也被称为 Graßmann 积。
这样,当a和e为零时,两者乘积可以写成,
$$ q1q2 = [− \vec{v} \cdot \vec{u}, \vec{v} \times \vec{u} ]$$
同纯虚数的说法,这时q1和q2叫纯四元数。
共轭性质
与二元虚数类似,四元数的共轭也是将虚部方向取反,即 $q^* = a - bi - cj - dk$,则
$$
\begin{aligned}
qq^* & = [s,\vec{v}] \cdot [s,-\vec{v}] \\
& = [s^2 - \vec{v} \cdot (-\vec{v}), s(-\vec{v}) + s\vec{v} + \vec{v}\times(-\vec{v})] \\
& = [s^2 + \vec{v} \cdot \vec{v}, \vec{0}] \\
\end{aligned}
$$
实部平方与虚部平方和,即该向量的模的平方,最后虚部为零,所以
$$
\begin{aligned}
qq^* & = [s^2 + \vec{v} \cdot \vec{v}, \vec{0}] \\
& = s^2 + |\vec{v}|^2 \\
& = a^2 + b^2 + c^2 +d^2 \\
\end{aligned}
$$
由于q与其共轭的积最后是个标量,为其模长,所以该乘法是满足交换律的。即$qq^* = q^*q = |q|^2$。
这样,
$$
q^*q = |q|^2 \\
\frac{q^*}{|q|^2}q =1
$$
则可以发现$q^{-1} = \frac{q^*}{|q|^2}$ 满足$q^{-1}q = qq^{-1} =1$,即为该四元数的逆。
而单位四元数的逆即为其共轭四元数。
三维旋转
旋转轴$\vec{u}$不妨设为单位向量,与之前的旋转类似,
$$ \vec{v’} = \vec{v’_{||}} +\vec{v’_\bot} = \vec{v_{||}} +\vec{v’_\bot}
$$
之前计算过正交与旋转轴的向量旋转得到的结果,$$\vec{v’_\bot} = \vec{v_\bot}cos\theta + (\vec{u}\times \vec{v_\bot})sin\theta$$
设u,v都是纯四元数,即$u = [0,\vec{u}]$,$v = [0,\vec{v}]$,两个纯四元数的Graßmann积为$$uv_\bot = [− \vec{v_\bot} \cdot \vec{u}, \vec{v_\bot} \times \vec{u} ] = [ 0, \vec{v_\bot} \times \vec{u} ] = \vec{v_\bot} \times \vec{u} $$
也是一个纯四元数。
所以,
$$
\begin{aligned}
v’_\bot & = v_\bot cos\theta + (u v_\bot)sin\theta \\
& = (cos\theta + usin\theta)v_\bot
\end{aligned}
$$
令四元数$q = (cos\theta + usin\theta)v_\bot$,则$ v’_\bot = qv_\bot$
所以对于垂直于旋转轴的向量,旋转$\theta$角度之后的向量可以用四元数的乘法来获得, 用向量表示为$q = [cos\theta, \vec{u}sin\theta]$
由于$\vec{u}$是单位向量,所以$$||q|| = cos^2\theta + ||\vec{u}||^2 sin^2\theta =1 $$
同样的表示方式,$qqv_\bot = q(qv_\bot)$几何上表示旋转两次,因此有$qqv_\bot = (cos2\theta + usin2\theta)v_\bot $
所以最后旋转之后的四元数,
$$\begin{aligned}
v’ & = v’_{||} + v’_\bot \\
& = v_{||} + qv_\bot \\
& = pp^{-1}v_{||} + ppv_\bot \\
& = pp^*v_{||} + ppv_\bot
\end{aligned}
$$
其中,$p = [cos(\frac{\theta}{2}),\vec{u}sin(\frac{\theta}{2})]$,是旋转半角的单位向量,因此$q=p^2$。
交换性质:
由之前的Graßmann积,上式中,将q写成向量形式,$q = [\alpha, \beta\vec{u}]$
$$ \begin{aligned}
qv_{||} & = [\alpha, \beta \vec{u}] \cdot [0,\vec{v}_{||}] \\
& = [-\beta \vec{u} \cdot \vec{v}_{||} , \alpha \vec{v}_{||} + \beta \vec{u} \times \vec{v}_{||}] \\
& = [-\beta \vec{u} \cdot \vec{v}_{||} , \alpha \vec{v}_{||}] \\
\end{aligned}
$$
右乘,
$$ \begin{aligned}
v_{||}q & = [0,\vec{v}_{||}] \cdot [\alpha, \beta \vec{u}] \cdot \\
& = [-\beta \vec{u} \cdot \vec{v}_{||} , \alpha \vec{v} +\vec{u} \times \vec{v}_{||}] \\
& = [-\beta \vec{u} \cdot \vec{v}_{||} , \alpha \vec{v} ] \\
& = qv_{||}
\end{aligned}
$$
再看垂直部分,
$$ \begin{aligned}
qv_\bot & = [\alpha, \beta \vec{u}] \cdot [0,\vec{v}_{}] \\
& = [-\beta \vec{u} \cdot \vec{v}_\bot , \alpha \vec{v}_\bot + \beta \vec{u} \times \vec{v}_\bot] \\
& = [0, \alpha \vec{v}_\bot + \beta \vec{u} \times \vec{v}_\bot] \\
\end{aligned}
$$
右乘共轭,
$$ \begin{aligned}
v_\bot q^* & = [0,\vec{v}_\bot] \cdot [\alpha, -\beta \vec{u}] \cdot \\
& = [-\beta \vec{u} \cdot \vec{v}_\bot , \alpha \vec{v}_\bot + \beta \vec{u} \times \vec{v}_\bot] \\
& = [0, \alpha \vec{v}_\bot + \beta \vec{u} \times \vec{v}_\bot] \\
& = qv_\bot
\end{aligned}
$$
所以旋转之后的结果可以化简为
$$\begin{aligned}
v’ & = pp^*v_{||} + ppv_\bot \\
& = pv_{||}p^* + pv_\bot p^* \\
& = p(v_{||} + v_\bot) p^* \\
& = pvp^*
\end{aligned}
$$
实际上,从计算过程可以看出,对于平行分量,乘$pp^*$,实际上是没有变化,对于垂直分量,乘$pp$,旋转了$\frac{\theta}{2} + \frac{\theta}{2} = \theta$角度。因此可以用旋转半角的四元数乘法来表示绕单位向量$\vec{u}$的旋转。
矩阵形式
单位向量$p= [cos(\frac{\theta}{2}), \vec{u}sin(\frac{\theta}{2})]$,以通用四元数方式表示为$p = a + bi + cj + dk$
其中$a=cos(\frac{\theta}{2}), b=u_x sin(\frac{\theta}{2}),c=u_y sin(\frac{\theta}{2}), b=u_z sin(\frac{\theta}{2})$
写成矩阵形式,之前说了四元数的矩阵形式左乘和右乘有点区别,左乘矩阵为
$$L=
\begin{bmatrix}
a & -b & -c & -d \\
b & a & -d & c \\
c & d & a & -b \\
d & -c & b & a
\end{bmatrix}
$$
右乘的矩阵等同于左乘矩阵
$$R = \begin{bmatrix}
a & -b & -c & -d \\
b & a & -d & -c \\
c & -d & a & b \\
d & c & -b & a
\end{bmatrix}
$$
所以有,
$$
\begin{aligned}
qvq^* & = L(q)R(q^*)v \\
& =
\begin{bmatrix}
a & -b & -c & -d \\
b & a & -d & c \\
c & d & a & -b \\
d & -c & b & a \\
\end{bmatrix}
\begin{bmatrix}
a & b & c & d \\
-b & a & -d & c \\
-c & d & a & -b \\
-d & -c & b & a \\
\end{bmatrix}
v \\
& =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1-2c^2-2d^2 & 2bc-2ad & 2ac+2bd \\
0 & 2bc+2ad & 1-2b^2-2d^2 & 2cd -2ab \\
0 & 2bd-2ac & 2ab+2cd & 1-2b^2-2c^2 \\
\end{bmatrix}
v \\
\end{aligned}
$$
矩阵最外圈不会有任何影响,所以可以得出向量$\vec{v}$绕单位向量旋转轴$\vec{u}$旋转的三维矩阵变换,即
$$\vec{v’} =
\begin{bmatrix}
1-2c^2-2d^2 & 2bc-2ad & 2ac+2bd \\
2bc+2ad & 1-2b^2-2d^2 & 2cd -2ab \\
2bd-2ac & 2ab+2cd & 1-2b^2-2c^2 \\
\end{bmatrix}
\vec{v}
$$
其中$a=cos(\frac{\theta}{2}), b=u_x sin(\frac{\theta}{2}),c=u_y sin(\frac{\theta}{2}), b=u_z sin(\frac{\theta}{2})$。